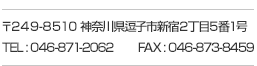中学3年生の数学の授業の様子をご紹介します。
本時は三角錐と展開図について学習していきます。
「前に授業内で扱った問題を、別の視点からも考えてみよう。」ということで、まずはプリントが配られます。
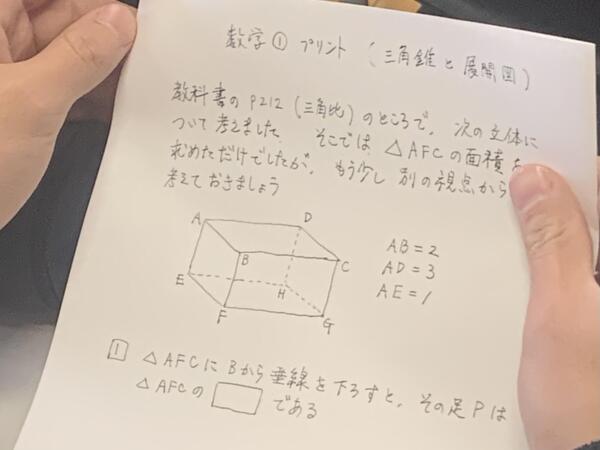
❶△AFCにBから垂線を下ろすとその点Pは△AFCの○○である。
この○○には「垂心」が入ります。
三角形の3つの頂点から各対辺に垂線を引くと1点で交わります。これが垂心です。
ですので、この点Pが△AFCの垂心であることを証明するには、AP,FP,CPが各対辺に垂直と言うことができれば良いのですね。


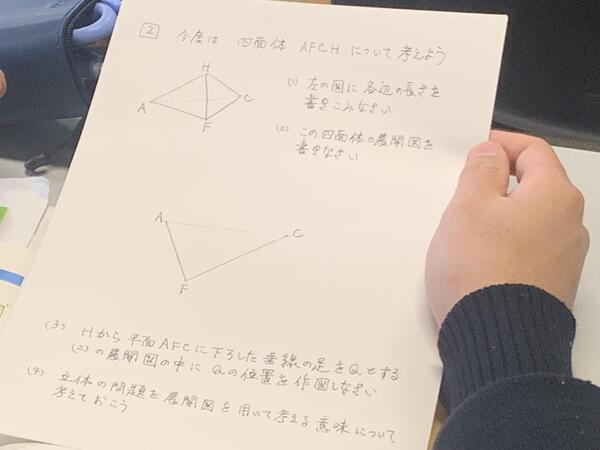
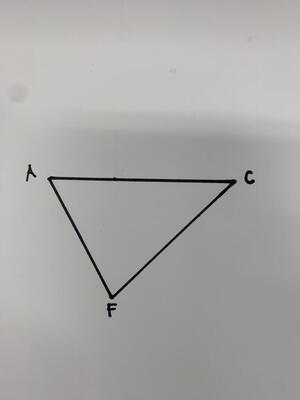
❷四面体AFCHについて
(2)この四面体の展開図を書きなさい。
展開図は以下のようになります。
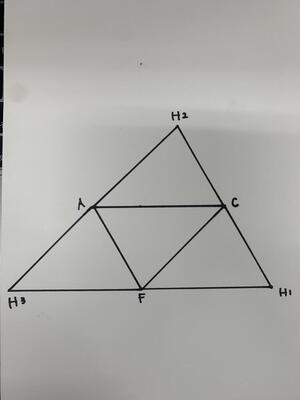
(3)Hから平面AFCに下ろした垂線の足をQとする。(2)の展開図の中にQの位置を作図しなさい。
この問題を解く前に、先生から三角形の紙が配られます。この三角形をつかって実際に三角錐を作りました。


①各辺の中点に印をつけます。
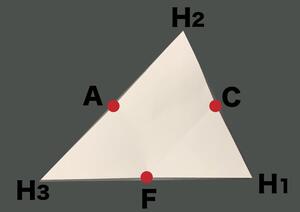
②中点を線で結びます。
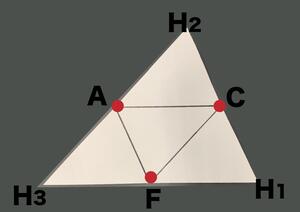
③線に合わせて折り、まずは三角錐の完成です。

④三角錐を作る時、真上から見て、H2がどの方向に動くか確認し、線を引きます。するとACに対して垂直となります。このときH1H3とも垂直になることに注意します。

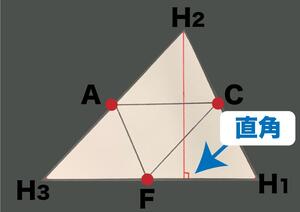
⑤H1,H3からも同様に線を引きます。これら3本の線は1点で交わるはずであり、それは△H1H2H3の垂心です。これが点Qの正体です。
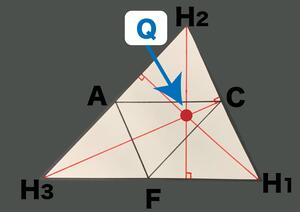
「おぉ!」「すごい!」「ほんとだ!」「わかった!」といろいろなところから声があがりました。


立体を頭の中だけで考えるのは難しい場合もありますが、このように一度展開してみて、それを組み立てるプロセスを観察することによって見通しが良くなることがあります。 こういう感動の積み重ねこそが、「数学が楽しい!」と思える瞬間をつくるのだろうと思いました。