12月8日(月)中学1年生数学の授業

12月8日(月)、中学1年生の数学「図形の性質」の授業にお邪魔しました。テーマは不変量について。

まずは前回の復習です。
「N角形の内角の和が 180°×（N-2） で表せることを示せ」
という問題について、以下の3通りの方法で表すことができることを確認しました。

①三角形に分割する
②外角の和を利用する
③多角形の内部に点を取る

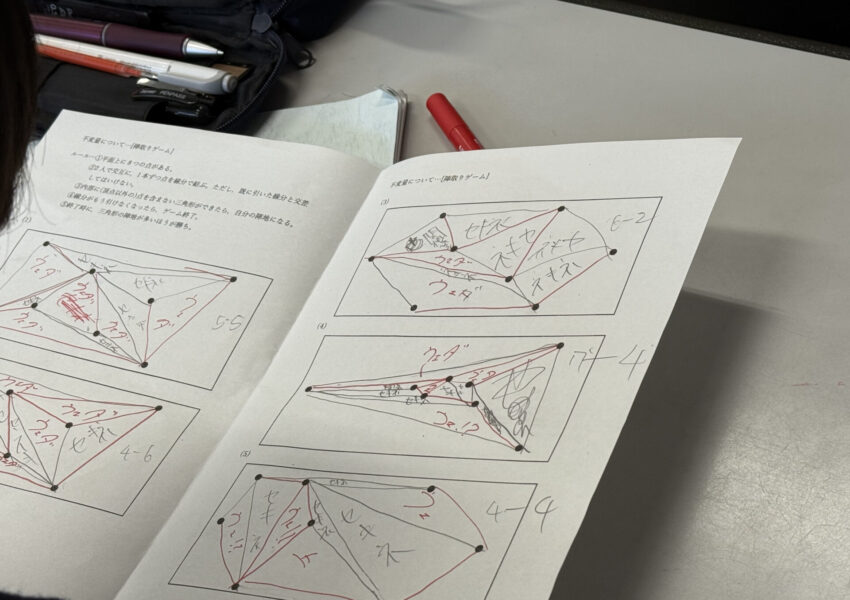
また、前回の授業ではプリントを使って陣取りゲームを行いました。
ゲームの結果、できた三角形の数は次のようになっていました。
(1)10個　(2)10個　(3)8個　(4)11個　(5)7個

さて、この三角形の個数はどうやって求めることができるのでしょうか？
2分間自分で考え、その後隣の席の人と話し合いをしました。

生徒たちは、図形全体を大きく捉え、次のことに気がつきました。
・(1)(2)…四角形の中に点が4つ
・(3)…六角形の中に点が2つ
・(4)…三角形の中に点が5つ
・(5)…七角形の中に点が1つ

つまり、外側の N 角形（頂点 N 個）と、その内部にある点 M 個から三角形の数が決まるという結論にたどり着きました。
ここからはさらに一歩進めて、
外側が N 角形で、内部に点が M 個あるとき、できる三角形の個数を M と N で表せ。
という問いに挑戦します。

生徒たちが「難しい〜！」と声をあげる中、先生が「わかりにくいときは、具体的な数字を当てはめて考えてみよう」とアドバイス。
まずは N＝8、M＝0 の場合から一緒に考えていきます。

N＝8、M＝0の場合、内部に点がないシンプルな八角形であることがわかります。八角形の内角の和は 1080°。
これを三角形1つの内角の和180°で割ると 6。

この1080°という八角形の内角の和こそ、どんな操作をしても変わらない量、不変量です。
つまり、八角形はどんな分け方をしても、必ず三角形が6個できるということになります。

それでは、内部に点があるとどう変わるのでしょうか？
N＝8、M＝1 の場合を考えてみます。
内部に点が1つ増えると、その点の周りに 360° 分の角が増えることになります。

つまり、点をつないでできる三角形の内角の合計＝外側の八角形の内角の和 ＋（内部の点まわりの360°）×点の数で表すことができます。

挙手した生徒が黒板に証明を書き進め、ついに、三角形の個数 はN − 2 + 2Mから求めることができる
という答えにたどり着きました。

今回の授業では、陣取りゲームを通して「数学は生活の様々なところに存在する」ということを実感しました。
考えるプロセスを大切にしながら、自分の手で法則を発見していく。そんな、数学の楽しさが詰まった素敵な授業でした。